Effetto cannocchiale: più ti allontani e più appare grande

Nulla di magico o misterioso: i tanti casi di architetture che sembrano ingrandirsi tanto più ci allontaniamo (il cosiddetto effetto-cannocchiale) dipendono semplicemente dal rapporto tra gli angoli con cui osserviamo l’oggetto e il contesto che lo circonda.

Alcuni esempi sono molto famosi, ad esempio il Cupolone di Roma da via Piccolomini. Più si va in direzione opposta alla cupola di San Pietro e più questa sembra riempire lo sfondo del viale tra gli alberi.

Molto noto anche il “cannocchiale di Bologna“, ossia la vista sulla Torre degli Asinelli dalla finestra dell’ex-monastero di San Michele in Bosco (oggi Istituto Ortopedico Rizzoli).
La prima immagine è la veduta in prossimità della finestra, la seconda è a metà del corridoio, la terza è nel punto più lontano (ovviamente, per fare il confronto, occorre usare un teleobiettivo).

Ho sperimentato anch’io qualcosa del genere anche in altri luoghi. Qui, ad esempio, siamo ad Atene, nel loggiato della Stoà di Attalo. Tra le colonne è possibile vedere il tempio di Efesto.

La prima foto è scattata in prossimità dell’apertura, usando un obiettivo grandangolare per includere la cornice attorno alla veduta. In questo caso il tempio appare piccolissimo, sullo sfondo. La seconda è fatta un po’ più indietro, usando un obiettivo normale. La terza dal punto più interno del loggiato, il più distante dall’apertura. Paradossalmente, in questo caso, il tempio occupa gran parte del riquadro.

In realtà non c’è nulla di paradossale e adesso vedremo perché.
Se osserviamo la pianta ci rendiamo conto che il tempio è sufficientemente lontano dal punto di vista da non subire sostanziali riduzioni dimensionali nel momento in cui un osservatore si porta qualche metro più indietro, nel punto più interno del loggiato.

Di contro l’apertura si rimpicciolisce molto più rapidamente, andando a circoscrivere una porzione di veduta più piccola. La differente velocità di rimpicciolimento inganna il nostro occhio e ci porta a pensare che l’oggetto sullo sfondo si debba essere necessariamente ingrandito. In verità anche il tempio è diventato un po’ più piccolo, ma molto meno della finestra.
Questo perché la nostra percezione delle cose è sempre relativa ai rapporti tra le parti. Non vediamo mai nulla in modo assoluto e isolato, ma sempre mettendo in relazione tra loro tutti gli elementi della scena.

Per capire ancora meglio l’effetto-cannocchiale, osserviamo questo semplice schema in pianta.

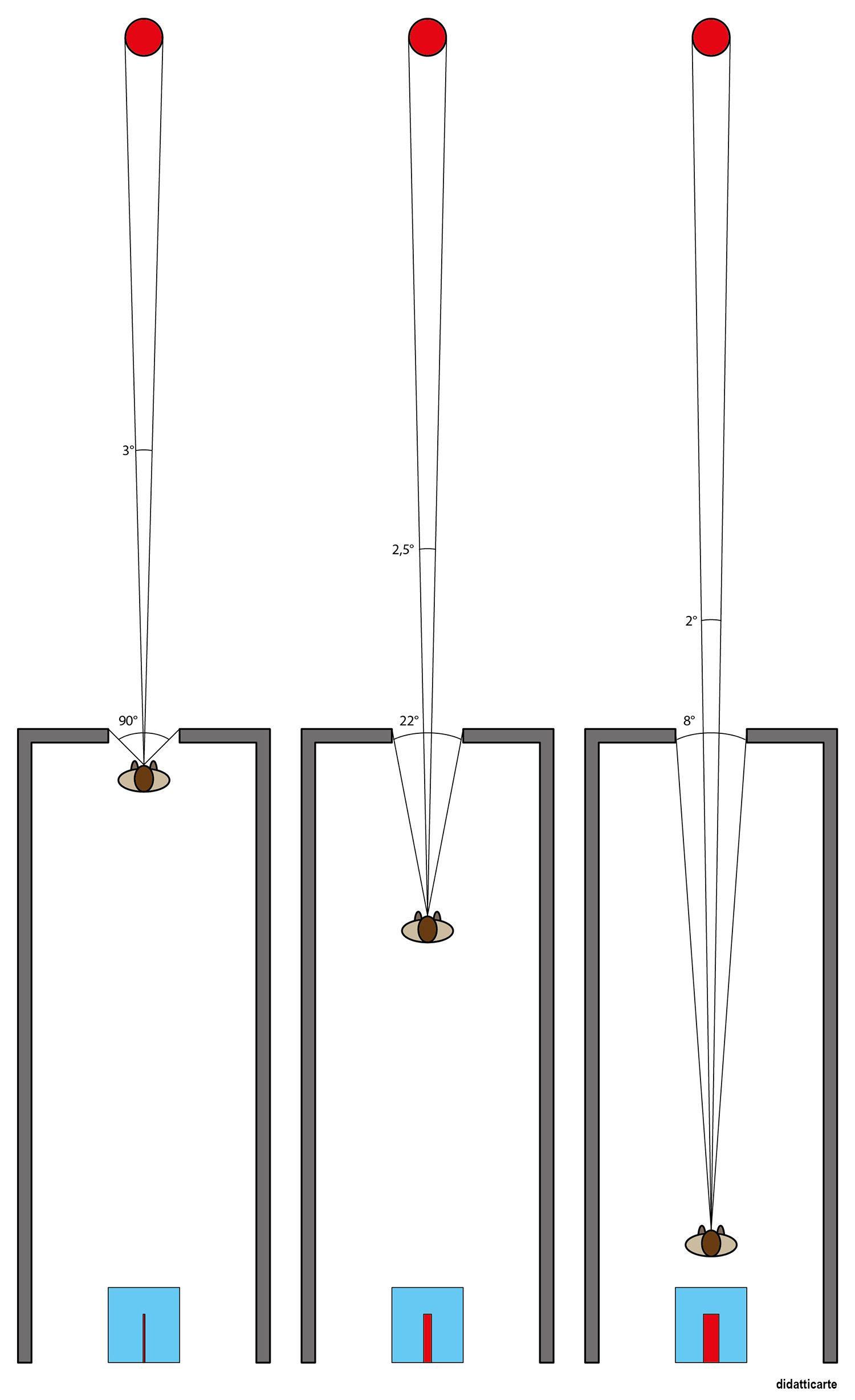
Nella prima immagine l’osservatore è prossimo alla finestra. L’angolo sotteso all’apertura è di 90° mentre quello entro cui vede l’oggetto rosso all’esterno è di 3°.
Nella seconda immagine, facendo pochi passi indietro, l’angolo con cui vede l’oggetto si è ridotto solo di mezzo grado, portandosi a 2,5° mentre quello entro cui vede la finestra è diminuito drasticamente, arrivando a 22°.
Nella terza immagine, andando ancora un po’ più indietro nel corridoio, l’angolo dell’oggetto rosso è diminuito fino a 2° ma quello della finestra è sceso a soli 8°.
La conseguenza è che, via via che ci si allontana, l’oggetto occuperà una porzione della cornice sempre maggiore (come si può vedere dai tre schemi inferiori), dandoci l’impressione che si sia addirittura ingigantito.

Si tratta evidentemente di un’illusione, ma pur conoscendone i meccanismi, non smette di affascinarmi e ogni volta che ne ho l’occasione provo a sperimentarla.
Questa è una prova che ho fatto ad Agrigento, inquadrando il retro del Tempio della Concordia attraverso un arco. Anche se appare controintuitivo, per ottenere la terza foto mi sono messa più lontano possibile dall’arco (chiaramente usando un po’ di zoom), mentre la prima l’ho fatta proprio a ridosso dell’apertura e la seconda in una posizione intermedia.

Pare che Robert Capa, il grande fotografo, dicesse: “Se la foto non è buona, vuol dire che non eri abbastanza vicino“.
Beh, quando si tratta di finestre attorno a un’architettura, il consiglio è quello opposto: se la foto non è buona, vuol dire che non eri abbastanza lontano!