Geometria e arte: i solidi platonici
Cosa c’entra un grande filosofo greco con un gruppo di cinque poliedri regolari? Tutto, soprattutto se il personaggio in questione si chiama Platone e se consideriamo la natura estremamente concettuale della geometria.
Ma di che poliedri parliamo esattamente? Occorre essere precisi: i cinque solidi platonici, infatti, presentano alcune caratteristiche che nessun altro possiede. La prima è che sono formati solo da poligoni regolari, nello specifico da triangoli equilateri, quadrati o pentagoni. In particolare, il tetraedro, l’ottaedro e l’icosaedro sono formati rispettivamente da quattro, otto e venti triangoli, l’esaedro (o cubo) da sei quadrati e il dodecaedro da dodici pentagoni. Ma occorre anche una seconda caratteristica, e cioè che sono tutti uguali tra loro anche gli angoloidi, cioè gli angoli solidi racchiusi tra tre o più lati.
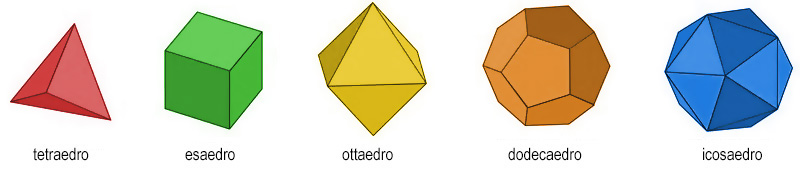
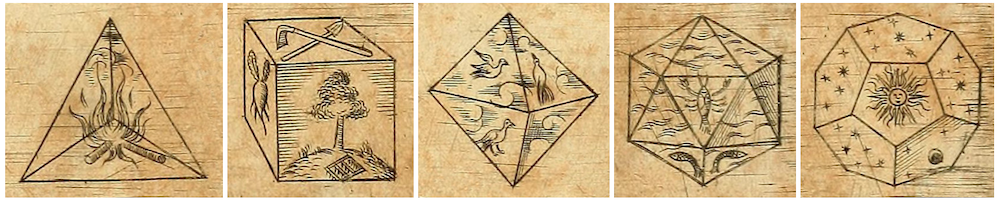
I solidi platonici, inoltre, sono gli unici poliedri convessi che possono essere iscritti in una sfera, cioè hanno tutti i vertici giacenti sulla superficie della sfera stessa. Il fascino di questi poliedri e la loro unicità furono apprezzati già in tempi antichi. Pare che Pitagora avesse già scoperto le proprietà delle ‘figure cosmiche‘ mentre Platone le ha associate agli elementi fondamentali. Nel “Timeo” (360 a.C.) collega il tetraedro al fuoco, il cubo alla terra, l’ottaedro all’aria e l’icosaedro all’acqua.
Il dodecaedro, invece, è simbolo dell’universo. Questa speciale attribuzione deriva dalla presenza del pentagono, figura che – contenendo in sé la sezione aurea – racchiudeva più di ogni altra l’idea di armonia e perfezione matematica.
I cinque poliedri ritornano con un approccio più matematico nel XIII libro degli “Elementi” (300 a.C.) di Euclide. Lo studioso riesce a dimostrare che non possono esistere più di cinque poliedri regolari e ne individua le formule per il calcolo dello spigolo, del volume e della superficie in relazione al diametro della sfera circoscritta.

Tuttavia, prima dell’antica Grecia, i solidi platonici erano già comparsi nel Neolitico in forma di pietre tondeggianti (dette petrosfere) ritrovate in Scozia e risalenti al 2.000 a.C. Il numero di ‘pomelli’ presenti sulla superficie rimanda in gran parte degli esemplari al numero di facce dei solidi platonici.

Si tratta di oggetti piuttosto misteriosi, così come i dodecaedri romani, strani solidi metallici dotati di piccole sfere lungo i vertici e grossi fori al centro di ogni faccia.

Dopo l’età classica i solidi platonici tornano in voga – ovviamente – nel Rinascimento. Stavolta però, oltre i matematici, interessano anche gli artisti.
Tra i primi va ricordato Paolo Uccello, pittore ed esperto di prospettiva che sul pavimento della basilica di San Marco a Venezia ha realizzato intorno al 1430 una splendida tarsia marmorea con il disegno di un inedito dodecaedro stellato (cioè dotato di una piramide su ogni faccia).

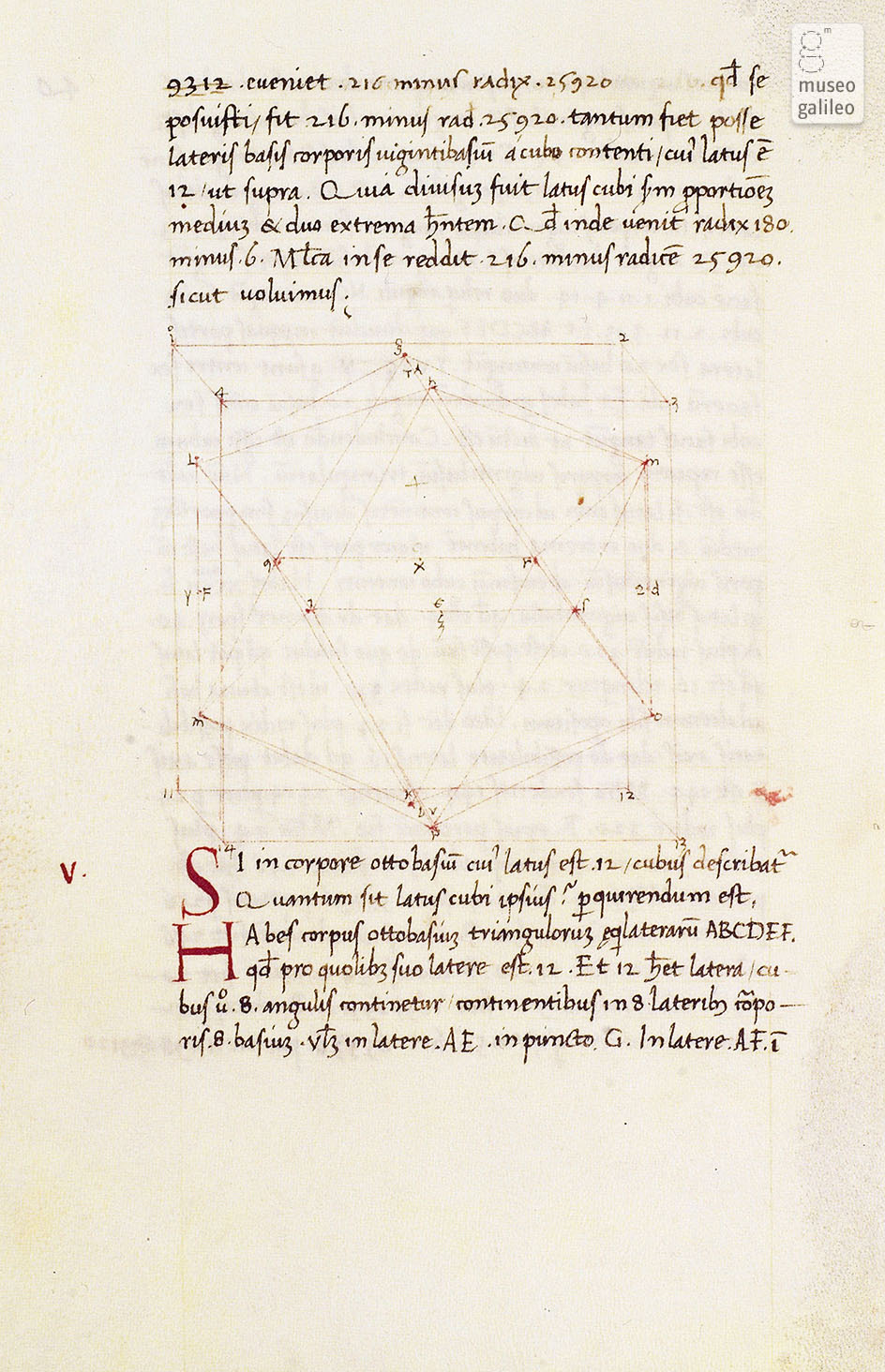
Piero della Francesca dedica ai cinque poliedri un intero trattato dal titolo “De quinque corporibus regularibus“. Nel testo, scritto intorno al 1480, il pittore sostiene che il mondo è costituito da volumi di forme complesse e irregolari ma che sono tutti riconducibili ai solidi platonici, forme basilari eterne e perfette.
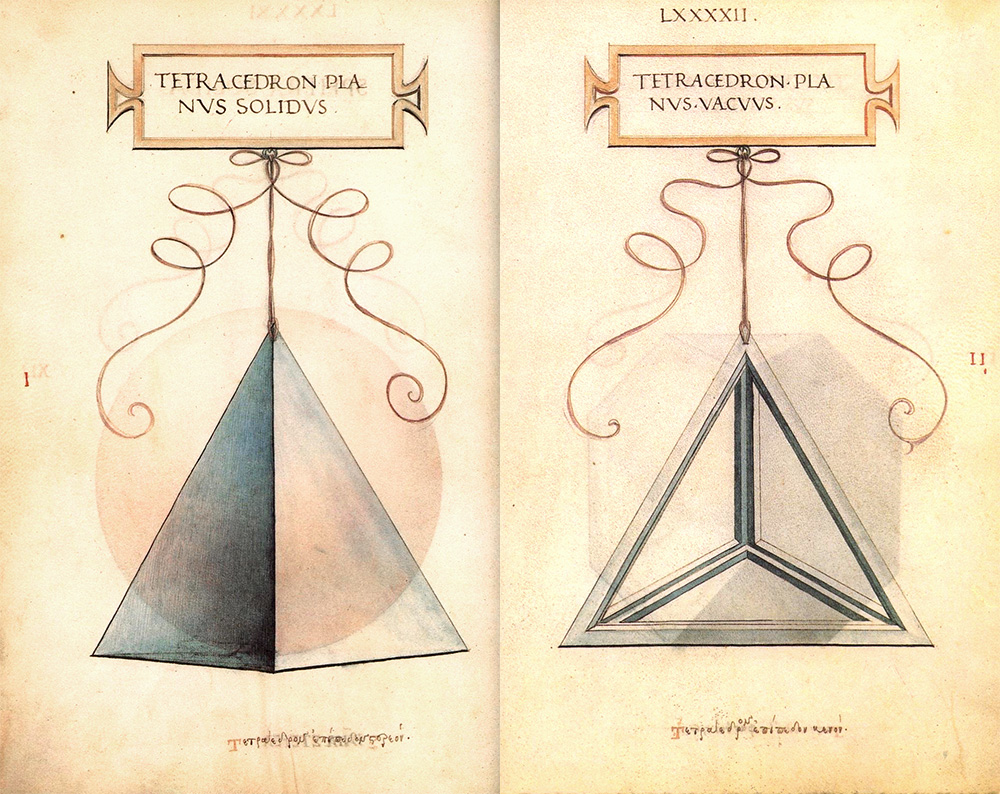
Pochi anni dopo Leonardo da Vinci disegna i solidi platonici, assieme a tanti altri poliedri, a corredo del “De divina proportione” (1509) del matematico Luca Pacioli. Nei suoi splendidi acquerelli ogni poliedro è appeso con una cordicella ad un cartiglio recante il nome latino del solido stesso (alla base del foglio, invece, è riportato il nome in greco). Di ognuno ha realizzato una versione piena (solidus) e una vuota (vacuus). Ecco il tetracedron.
Segue l’exacedron.
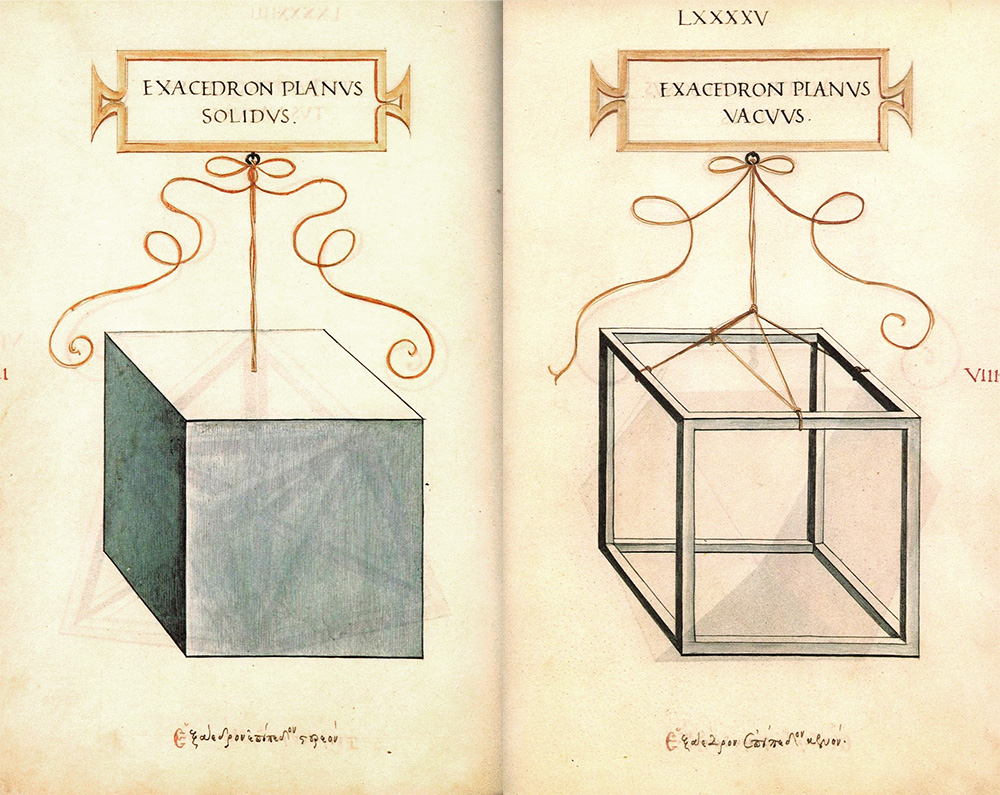
Poi c’è l’octocedron.
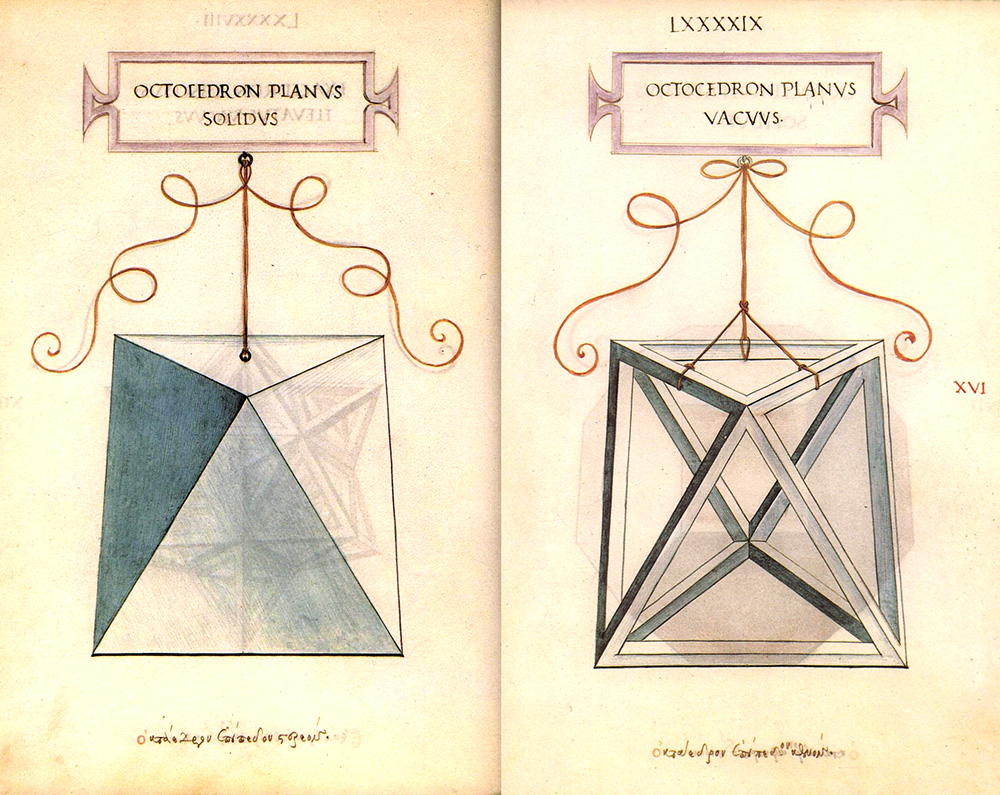
E ancora il duodecedron.
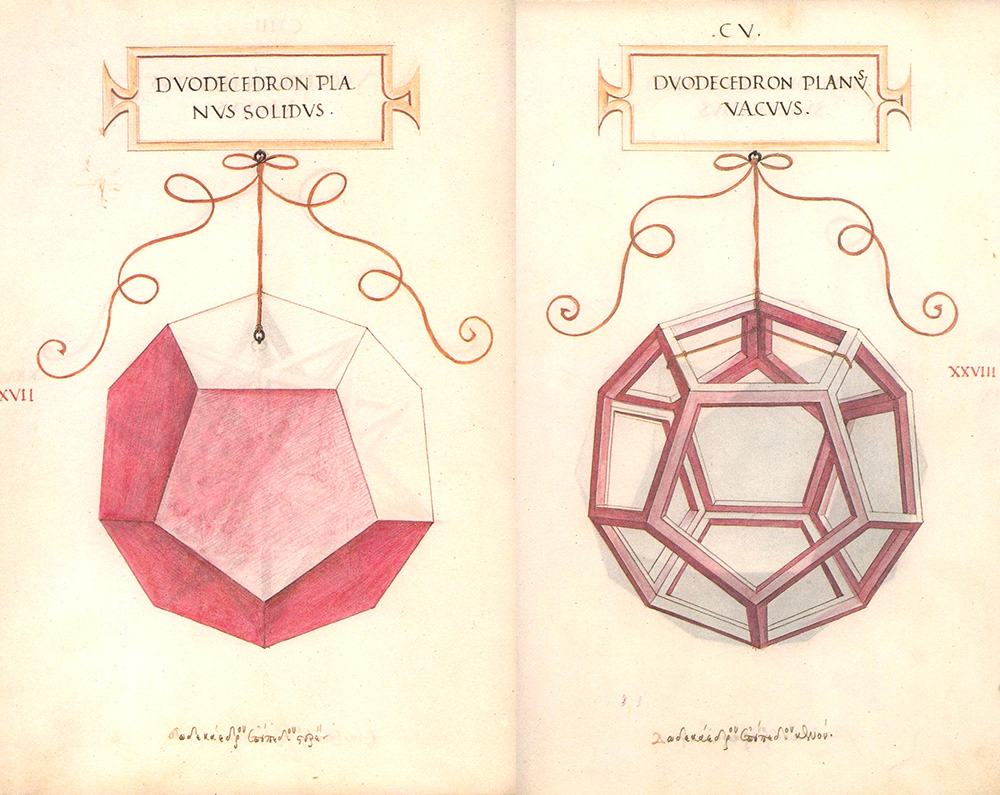
E infine l’ycocedron.
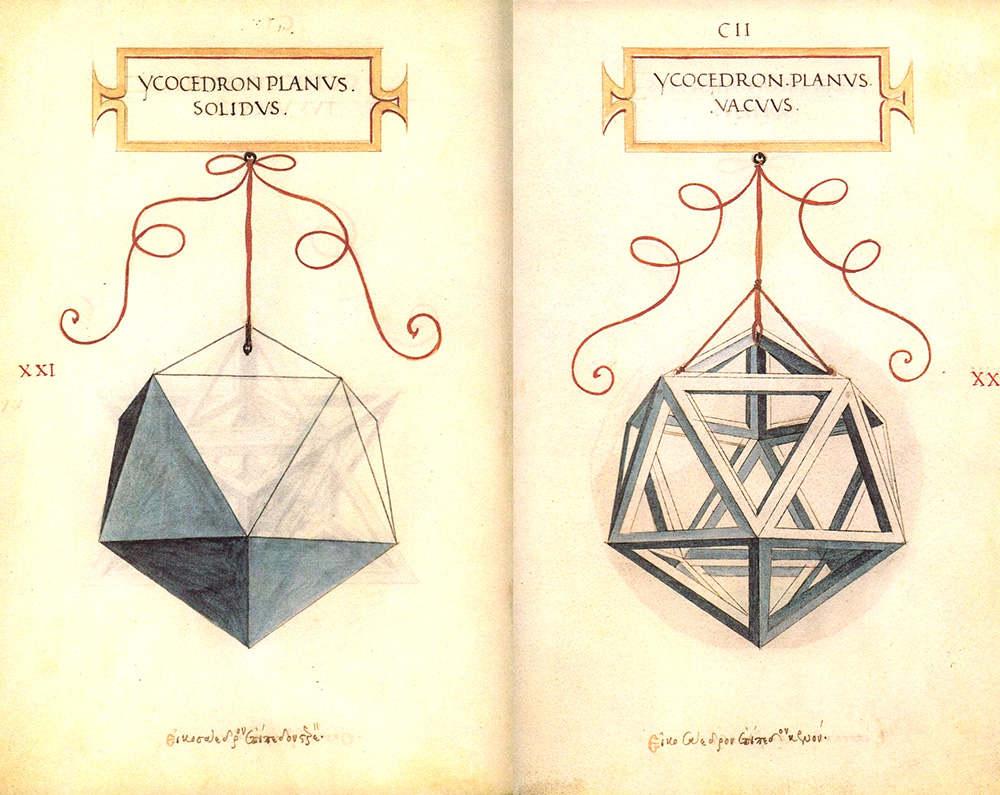
Pochi anni dopo anche il tedesco Albrecht Dürer si occupa di poliedri. È celebre quello presente nell’incisione Melancolia I del 1514. Non è un solido platonico ma sembra averne tutto il fascino.

Successivamente, con il suo “Underweysung der Messung mit dem Zirckel und Richtscheyt” (1525) (Istruzioni per misurare con riga e compasso) Dürer disegna lo sviluppo di alcuni poliedri, cioè la figura piana che si ottiene separando alcuni spigoli tra le facce. Ecco lo sviluppo del dodecaedro e le sue viste di fianco e dall’alto.
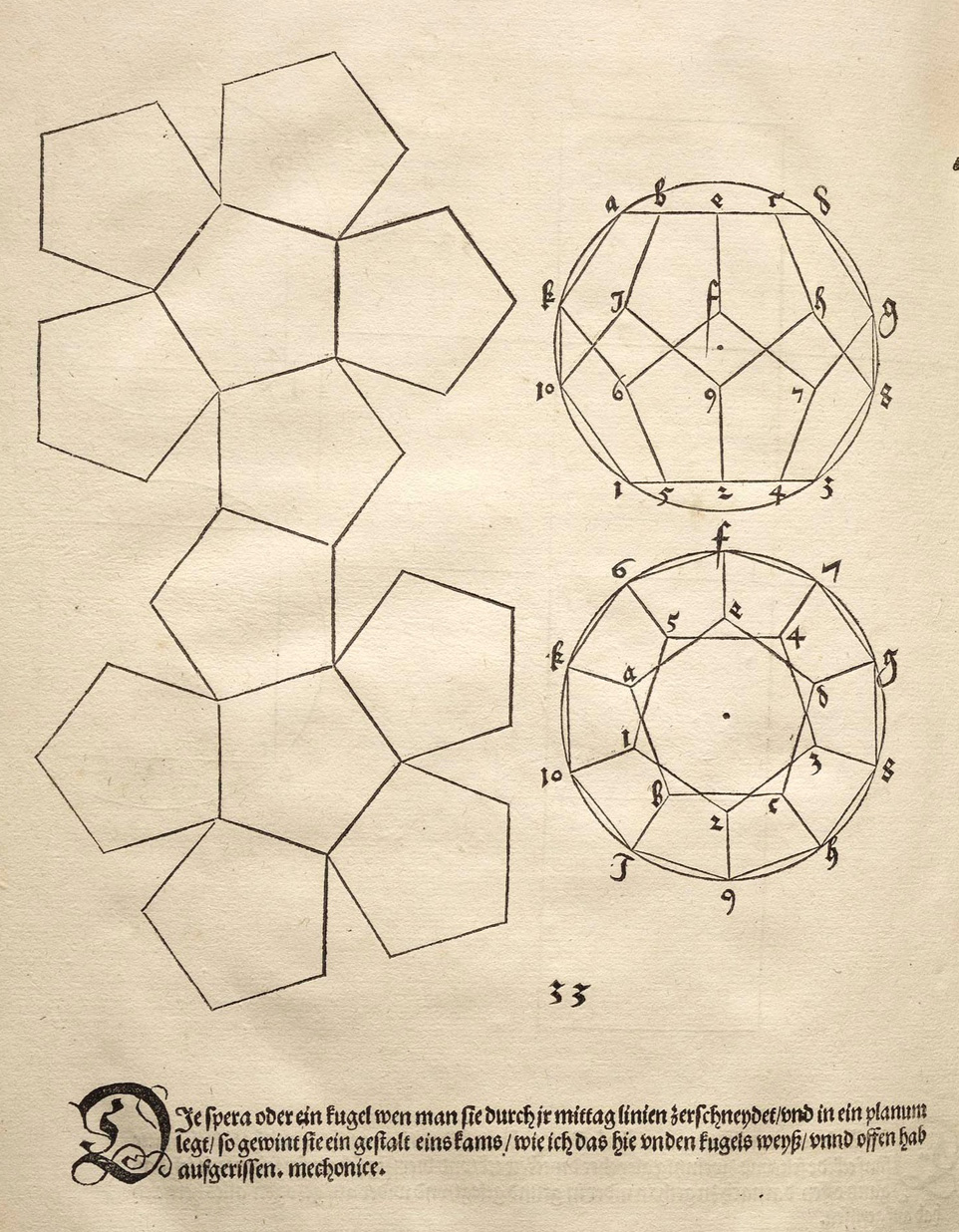
Qualcosa di simile è stato prodotto anche da Augustin Hirschvogel, un artista e matematico tedesco, autore del trattato “Geometria” (1543) da lui stesso illustrato.
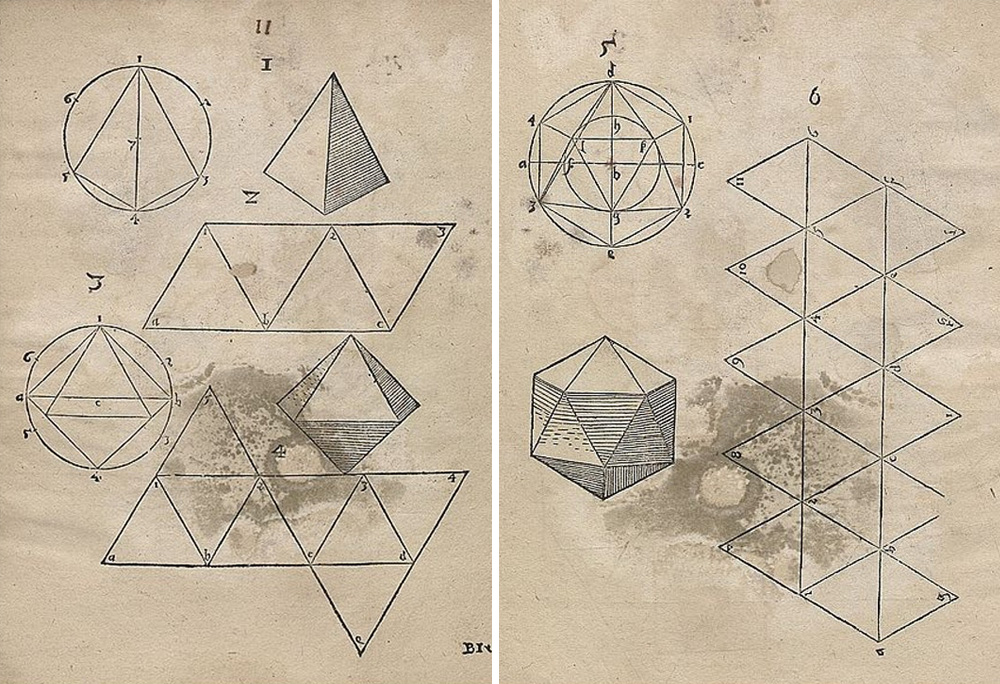
Decisamente più artistiche sono le tavole di Lorenz Stoer contenute nel suo Geometria et Perspectiva (1567). In questo caso i solidi platonici sono ambientati dentro paesaggi geometrici che sembrano anticipare le visioni matematiche di Escher.

Dopo la metà del secolo è il turno dell’incisore tedesco Wenzel Jamnitzer che nel suo “Perspectiva corporum regularium” (1568) analizza tutte le possibili varianti dei cinque solidi platonici, incluse le versioni stellate o troncate (cioè con i vertici tagliati). Il totale è di ben 120 poliedri: un’immaginifica collezione di forme impensabili che si colloca esattamente a metà tra scienza e arte e che vuole dimostrare l’assunto di Platone e cioè che ogni solido discende dai cinque originari. Queste sono due tavole con alcune variazioni sull’icosaedro.
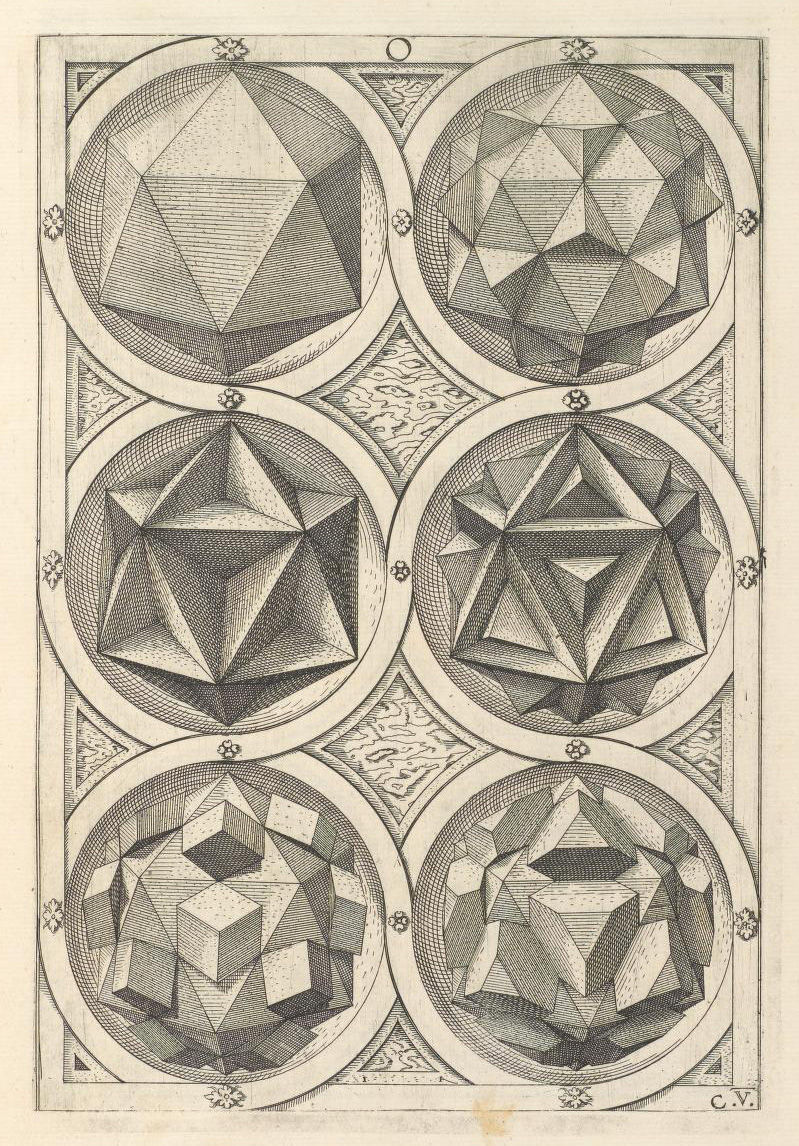

Mentre questi sono alcuni esempi di variazioni del dodecaedro.
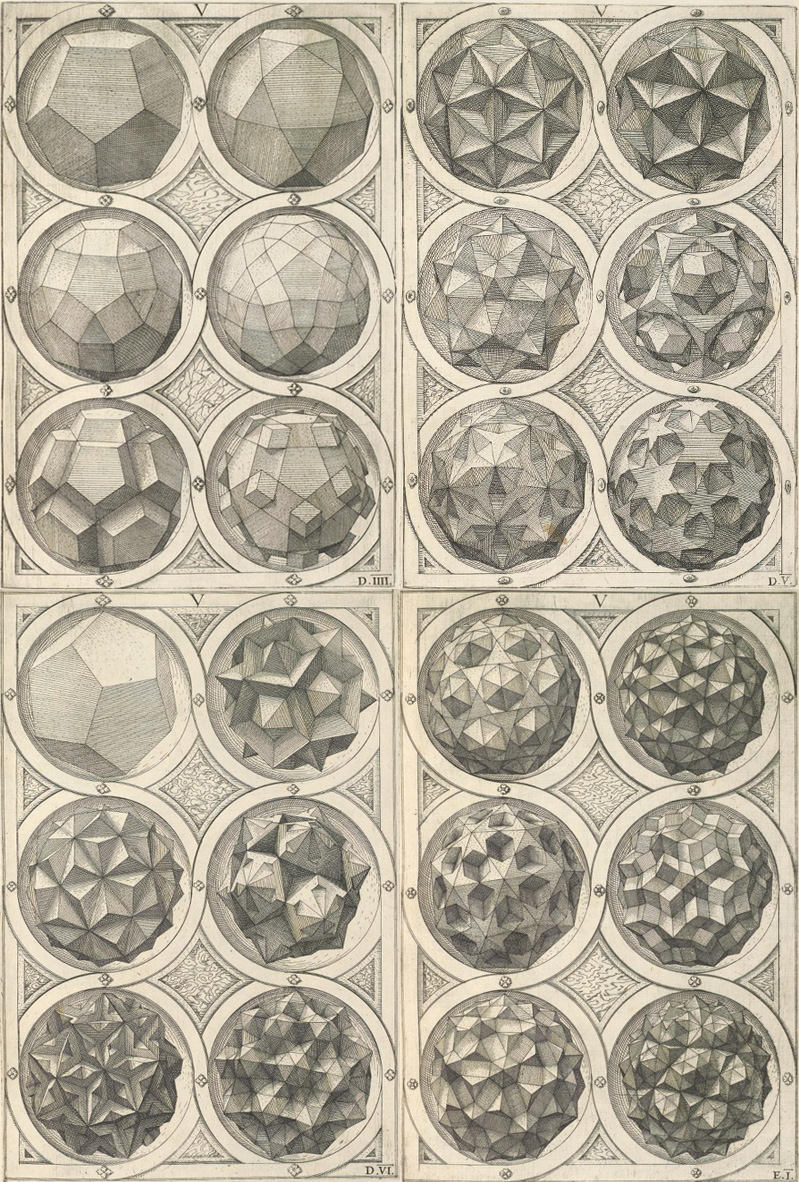
Osservare questi disegni è provare visivamente la vertigine del calcolo combinatorio, con la differenza che le possibilità di trasformazione dei solidi platonici sono potenzialmente infinite.
Della stessa epoca, ma di autore ignoto, sono alcuni disegni acquerellati in cui poliedri più o meno complessi sono accompagnati da uccelli o altri piccoli animali. L’effetto, delicato e straniante allo stesso tempo, è incredibilmente surreale.

Pochi anni dopo, le teorie di Platone verranno riprese da Keplero che nel suo “Mysterium Cosmographicum” (1597) immagina il sistema solare come un insieme concentrico di solidi platonici, le cui proporzioni determinano le distanze e le posizioni dei pianeti. La rappresentazione grafica di questo concetto è stata realizzata da Christophorus Leibfried.
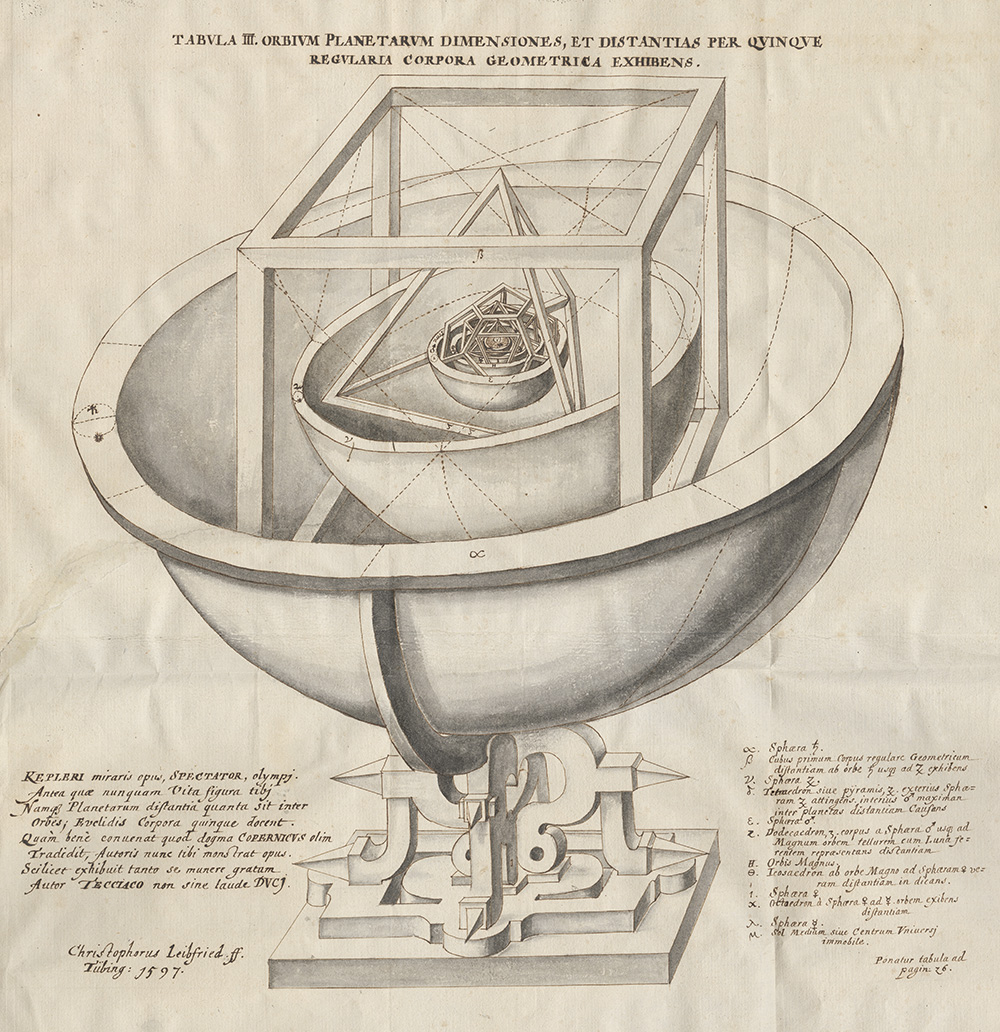
Con “Harmonices Mundi” del 1619 Keplero torna ad occuparsi dei solidi platonici alla ricerca del concetto di armonia e bellezza geometrica. È in questo testo che teorizza i poliedri non convessi (inclusi quelli stellati) che oggi portano il suo nome.

Nel 1900 è la volta del matematico tedesco Max Brücker, autore di “Vielecke und Vielflache: Theorie und Geschichte” (Poligoni e poliedri: teoria e storia). Il suo testo, una summa di tutto ciò che si sapeva fino a quel momento sulla materia, è accompagnato da centinaia di incisioni e dalle foto di 146 spettacolari modelli in carta dei vari solidi.

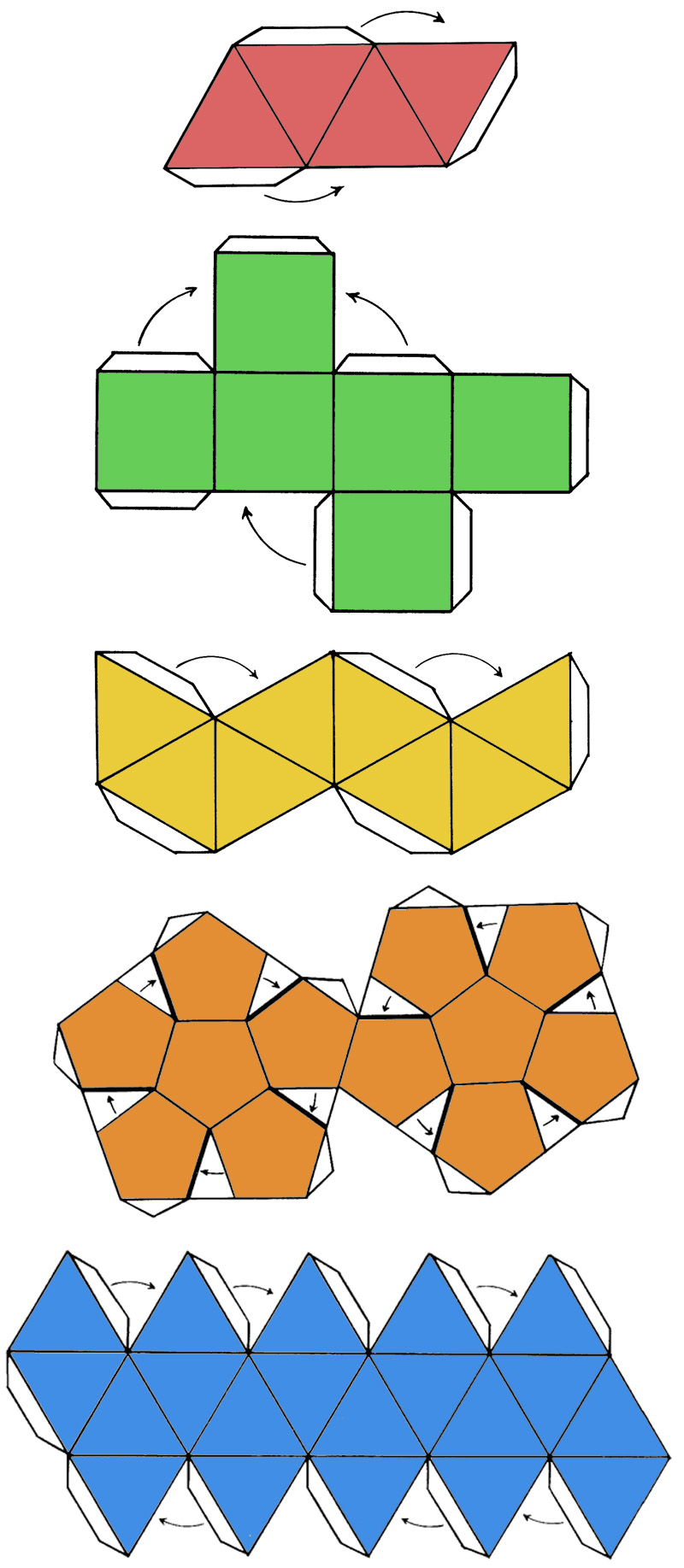
Quella del modellino tridimensionale è un’attività che, in piccolo, si può fare anche a scuola. Basta disegnare su carta lo sviluppo dei solidi con le apposite linguette e incollare i vari lati. L’importante è essere estremamente precisi nella geometria delle varie facce.

I solidi platonici e le loro versioni stellate saranno una delle passioni di Maurits Cornelis Escher. E proprio “Stelle” si intitola una xilografia del 1948 in cui l’artista olandese mette assieme il camaleonte, simbolo di trasformazione, il concetto platonico di eterna perfezione dei poliedri e l’evocazione del cosmo. Il solido centrale, vuoto come quelli di Leonardo, è un originale incastro di tre ottaedri.

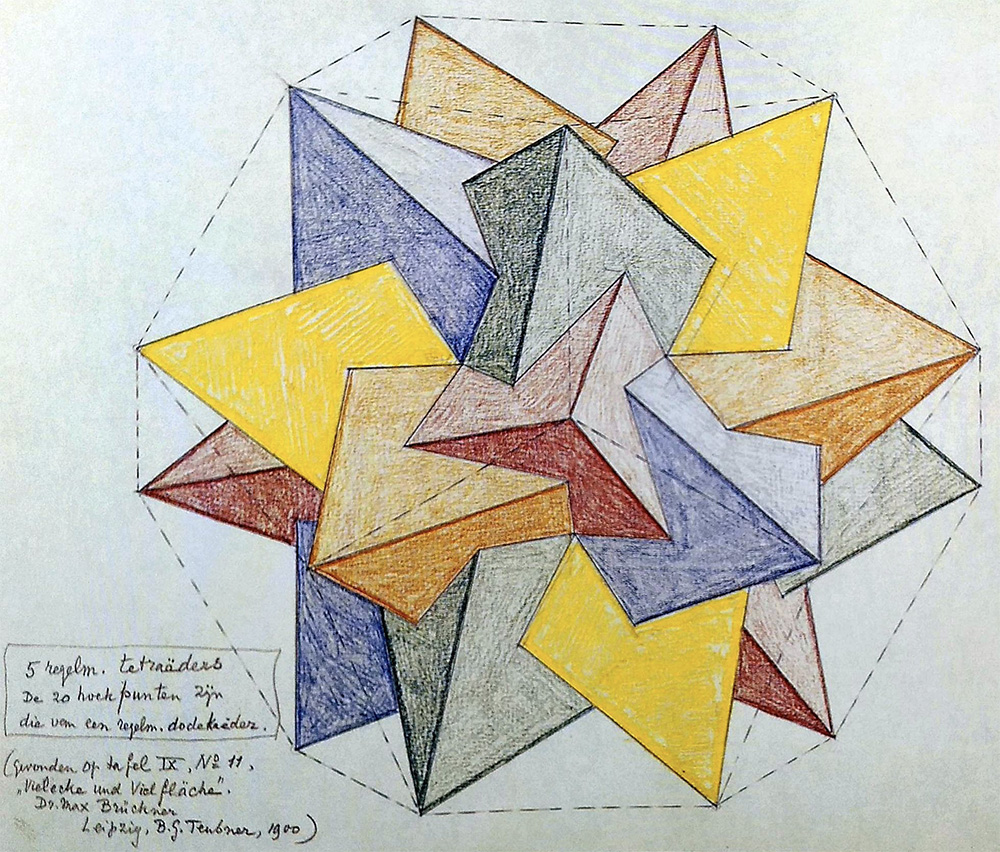
Quello di “Stelle” non è l’unico poliedro nato da un incastro. In questo schizzo Escher è riuscito a mettere assieme ben cinque tetraedri! Solo grazie al colore riusciamo a individuare i singoli solidi che lo compongono.
Con “Cristallo”, del 1947, Escher incastra un cubo e un ottaedro per creare un oggetto dalla geometria purissima da contrapporre alla massa informe della ghiaia. Di questi solidi quasi astratti l’artista diceva: “Essi simbolizzano il desiderio di armonia e di ordine dell’uomo, ma nello stesso tempo la loro perfezione desta in noi il senso della nostra impotenza. I poliedri regolari non sono invenzioni della mente umana, perché esistevano molto prima che l’uomo comparisse sulla scena“.

La stessa esaltazione della perfezione dei poliedri è il tema di “Contrasto (ordine e caos)” del 1950. Il solido, un dodecaedro stellato quasi trasparente, è parzialmente inglobato in una sfera di vetro. Attorno a questo simbolo di bellezza matematica solo oggetti rotti, a rappresentare il caos che si contrappone all’ordine.

In tempi più recenti si trovano i dipinti di Lucio Saffaro, pittore, scrittore e matematico che tra gli anni Ottanta e Novanta ha fatto dei solidi platonici e delle loro varianti i soggetti unici di tele dal sapore metafisico.

Questi solidi, così nitidi, così assoluti, confermano il pensiero di Bertrand Russel a proposito del rapporto tra matematica e arte: “La matematica, vista dalla giusta angolazione, possiede non solo verità ma anche suprema bellezza, una bellezza fredda e austera, come quella della scultura, sublimamente pura e capace di una perfezione austera, come solo la grande arte può mostrare“.






Grazie Emanuela!!! Anche la matematica ha un alone di fascino e mistero ; )
Buone Feste. Elisa
Grazie a te. E tanti auguri!
Quando facevo le elementari si trovavano i cartoncini da ritagliare coi vari solidi,peccato che poi nel corso degli studi superiori nessuno ne abbia più fatto cenno,un entusiasmante esempio di interdisciplinarità
Complimenti, Emanuela. Veramente un lavoro molto interessante e per me, a tratti, ostico. Ma studierò!!!
Grazie Ugo, è più semplice di quanto immagini. E soprattutto è estremamente affascinante!
Molto interessante
al solito: fantastica.
❤️
Ottimo! Ho iniziato a presentare Piero della Francesca e il tuo lavoro sarà un interessante approfondimento. Grazie
Bellissime le immagini ma anche la descrizione
Ti ringrazio, Andrea.
Gli articoli di questo sito non mancano mai di meravigliare e di educare, lasciandoci sempre un po’ piu’colti e ispirati. Grazie
Grazie a te, Tina!
Articolo molto bello che tocca un tema a me molto caro. Insegno matematica e la geometria è la mia passione.
Inoltre sono una origamista. Moltissime delle variazioni, quasi surreali, dei solidi platonici sono realizzabili piegando la carta, senza tagli né colla. È un mondo da esplorare.
Un modello abbastanza classico dell’origami è quello dei 5 tetraedri incastrati di Hill.
Grazie per il suggerimento, Renata. Cercherò le istruzioni per l’origami!