Insegnare l’arte con la matematica

Tenetevi forte! Stavolta l’esperimento è veramente azzardato.

Quello che voglio raccontarvi oggi è un tentativo di spiegare la storia dell’arte attraverso concetti propri della matematica. Perché la matematica possiede un’esattezza, una forza di sintesi, un linguaggio simbolico che altre discipline non hanno. E così, ogni tanto, la uso per parlare di arte (tra lo sconcerto generale degli studenti…).

Prendiamo la trigonometria.

Prendiamo in particolare la funzione y = sen (x). Questa funzione, graficizzata sugli assi cartesiani, può rappresentare perfettamente il moto armonico di oscillazione di un pendolo in funzione del tempo. Il grafico sarà una sinusoide.

Sì, ma che me ne faccio di una sinusoide per spiegare la storia dell’arte? È presto detto: dalle origini fino all’Ottocento si può dire che il concetto di arte abbia sempre oscillato tra periodi classici e periodi anti-classici.

Detta così è un po’ grossolana, lo capisco. Però, se non prendiamo in modo troppo rigido questo schema, credo che possa essere di grande aiuto per cogliere in modo immediato l’alternarsi di sensibilità opposte riconducibili alla visione classica dell’arte e a quella contraria.

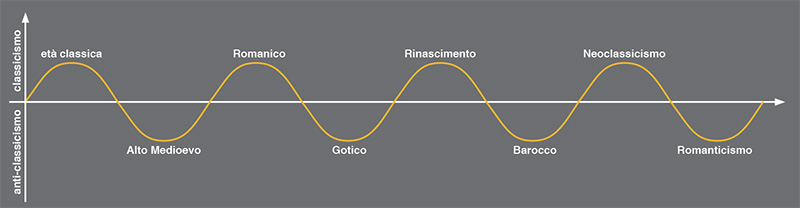
Sembra emergere un bisogno periodico di certezze, di misura, di staticità e di equilibrio che viene bilanciato successivamente da una tensione verso il deforme, l’eccessivo, il dinamico, il patetico.

Che poi anche all’interno di ogni periodo ci sono delle sotto-oscillazioni: l’arte classica, per esempio, comprende un periodo dell’arte greca definito, a sua volta, classico e uno ellenistico che sembra esserne l’opposto.

Così come durante l’Alto Medioevo (un periodo considerato anti-classico), con l’arte carolingia c’è una ripresa della classicità romana.

La sinusoide dell’arte però, a differenza di quella matematica che è teoricamente infinita, termina con la metà dell’Ottocento. Cosa succede? Forse che con l’Impressionismo saltano tutti i riferimenti all’arte precedente? Forse siamo entrati davvero nel contemporaneo?

Di sicuro l’Impressionismo, per quanto lezioso possa apparire, è stato un movimento rivoluzionario: per la prima volta la pittura si interroga sui suoi strumenti linguistici, sul colore, sulla luce, sulla visione. Paesaggi e scorci urbani diventano un pretesto per ripensare il concetto stesso di rappresentazione.

Ecco, il concetto di rappresentazione è fondamentale nella storia dell’arte. Il rapporto che ha l’uomo con la realtà è estremamente variabile.

Direi che può tendere verso due direzioni contrarie: verso la massima idealizzazione, una perfezione inesistente in natura, oppure verso il realismo più spietato, quello che mette crudemente in scena ogni forma di bruttura.

Come rappresentare in modo schematico queste opposte tensioni? Con un’iperbole, naturalmente! (per essere precisi solo il primo quadrante della funzione y = 1/x)

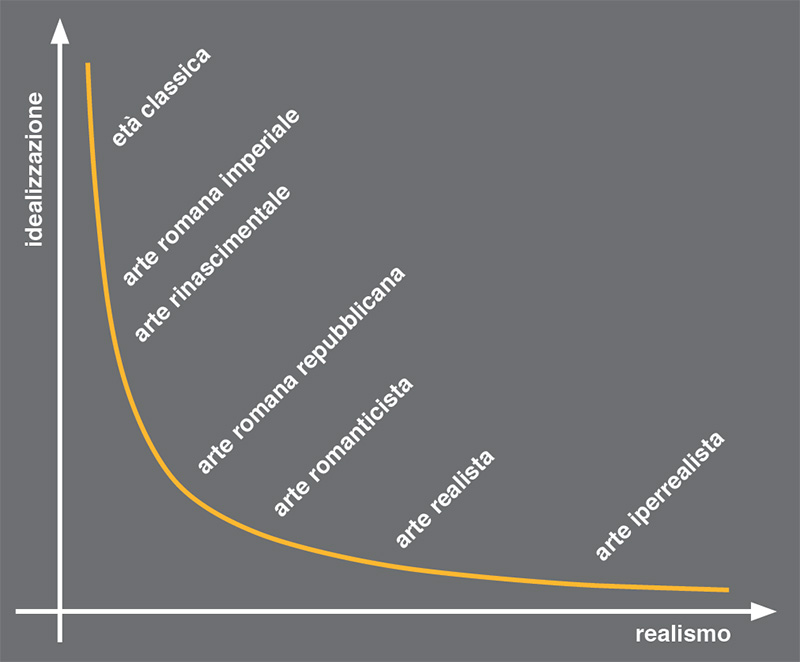
Chiaro che non sto dicendo che la storia dell’arte si possa spiegare tutta con formule matematiche.

Ma perché non raccontare, ad esempio, la tensione spasmodica verso un modello lontano e irraggiungibile utilizzando la metafora del limite di una funzione?

Oppure perché non usare gli insiemi e le loro intersezioni per cercare di visualizzare movimenti, autori e temi?

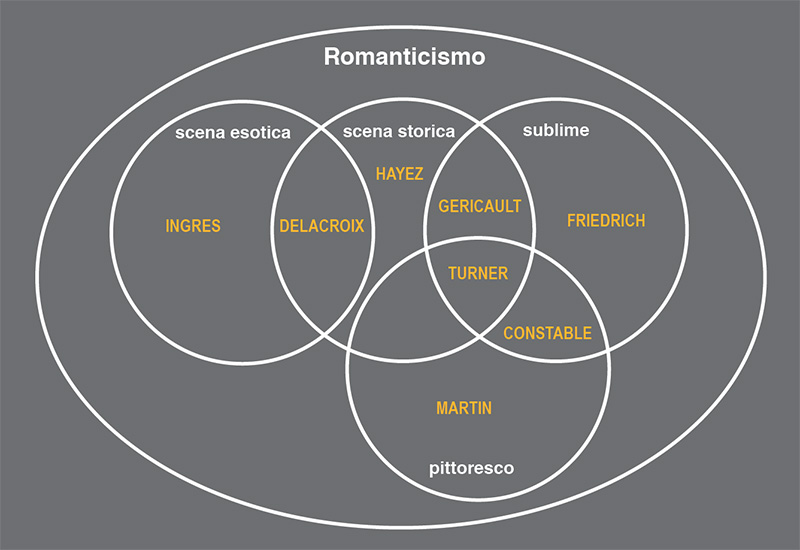
Sono consapevole del rischio di eccesso di semplificazione che queste rappresentazioni possono comportare. Manco a farlo apposta, proprio oggi Annamaria Testa ci spiega la differenza tra semplicità e semplicismo, dove il secondo è solo una barbara potatura dell’intricato bosco nel quale ci muoviamo mentre la prima implica il disegno di un tracciato leggibile in mezzo alla selva.

La vera sfida, comunque, non è proporre la storia dell’arte in modi sempre più bizzarri quanto portare gli studenti ad inventare il loro modo di raccontarla e di renderla semplice a se stessi.

Perché, come scrive ancora Annamaria, “per rendere semplice ciò che è complesso bisogna prima averlo studiato e capito bene. E poi bisogna trovare il modo per spiegarlo. Questo significa prendersi delle responsabilità, perché essere semplici vuol dire anche scegliere tra ciò che è davvero importante e ciò che non lo è”.